How (and why) do you build a scale using flat names instead of sharp names? In the last lesson, we learned how to build a one octave major scale. Recall these points…
- There are 8 notes in a one octave scale
- The first and last notes are always the same name
- The sequence of intervals from the first note is always
- Whole step
- Whole step
- Half step
- Whole step
- Whole step
- Whole step
- Half step
Recall also that we built a number of scales during the course of the lesson:
C D E F G A B C
G A B C D E F# G
D E F# G A B C# D
A B C# D E F# G# A
E F# G# A B C# D# E
B C# D# E F# G# A# B
Notice again that the first and last notes are always the same note. Notice also that each of the other letters in the scale occurs once and only once; it may be a sharp (#) or it may be a regular note but it happens only once in the scale sequence. None of the scales we have built so far have used a note with a flat name and that is the project I have for today’s lesson. So, let’s build an F scale.
From previous lessons, you know that the first note of the scale will be the name of the scale, in this case F. You also know that the interval from the first note to the second note has to be a whole step. Take a look at the following diagram and you will see that the interval between F and G is indeed a whole step.
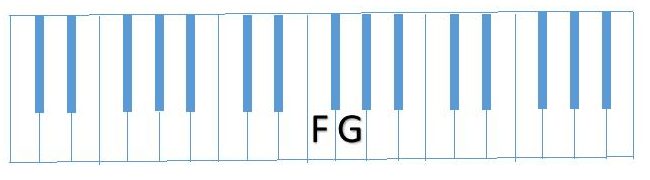
Thus far our scale sequence is F (whole step) G
You also learned in previous lessons that the interval from the second note to the third note has to be a whole step. A is a whole step from G.
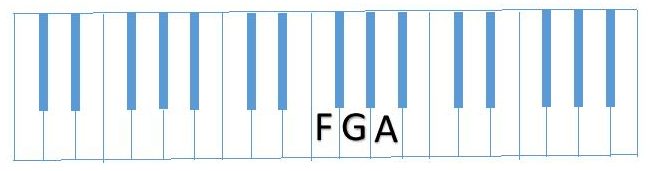
Our scale sequence is now F (whole step) G (whole step) A
We’re now ready to choose the fourth note of the scale. The previous lessons taught you that the interval from the third to the fourth note of the scale has to be a half step. What note is a half step up from A? Remember you can use a letter once and only once. If you said A# will be the fourth note, you’re only half right. A# is indeed a half step up from A, but you already used the letter A for the third note so you can’t use that letter again. You have to call the fourth note by it’s flat name Bb.
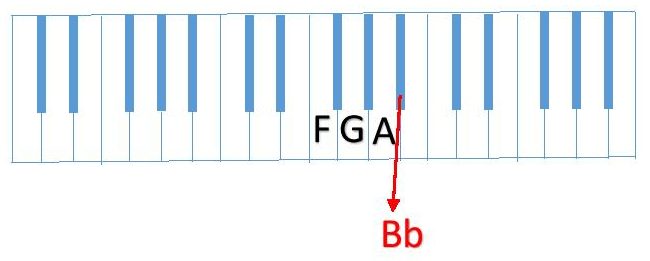
Our scale sequence is now F (whole step) G (whole step) A (half step) Bb
Recall that the fifth note of the scale must be a whole step from the fourth note. C is a whole step up from Bb.
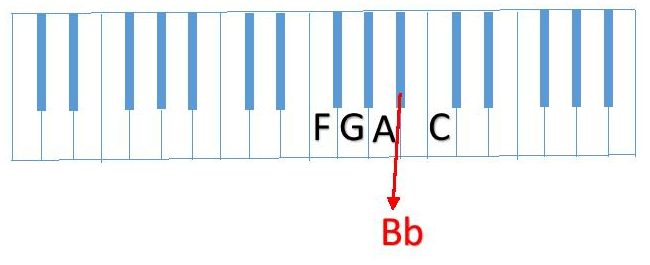
Our scale sequence is now F (whole step) G (whole step) A (half step) Bb (whole step) C
The sixth note of a major scale must be a whole step from the fifth note and D is a whole step up from C.
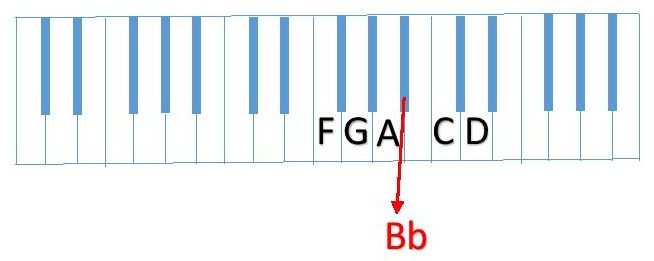
Our scale sequence is now F (whole step) G (whole step) A (half step) Bb (whole step) C (whole step) D
The seventh note of a major scale must also be a whole step from the sixth note. E is a whole step up from D.
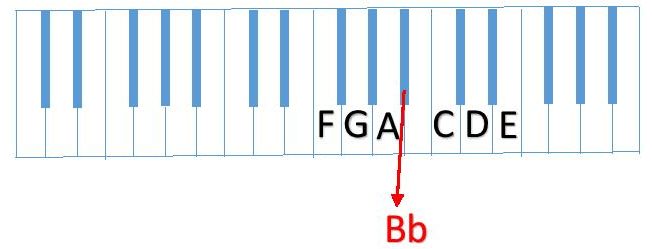
Our scale sequence is now F (whole step) G (whole step) A (half step) Bb (whole step) C (whole step) D (whole step) E
The eighth and final note of a major scale is only a half step from the seventh note. F is a half step up from E and, showing that everything is right and proper with the universe, completes the octave scale with the same note that begin the scale.
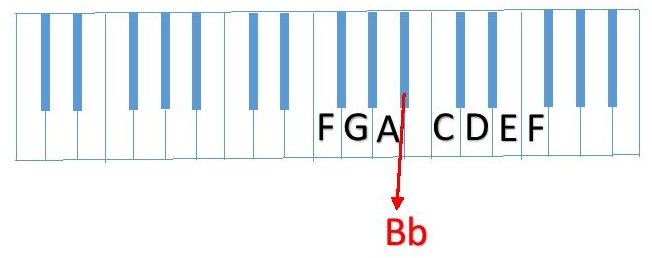
Our completed scale sequence is
F (whole step) G (whole step) A (half step) Bb (whole step) C (whole step) D (whole step) E (whole step) F
To summarize the points made in this lesson:
- There are 8 notes in a one octave scale
- The first and last notes are always the same name
- Each letter (other than first and last) must be used once but can only be used once.
- The sequence of intervals from the first note is always two whole steps, a half step, three whole steps, and a half step.
Now see if you can complete the following scales. Hint: first, fill in all the letters of each scale using each letter once and only once. Then add flats as needed to make the required sequence of whole steps and half steps. Answers are at the bottom of the page. Don’t peek.

Answer key for scales built using flats
| Bb | C | D | Eb | F | G | A | Bb |
| Eb | F | G | Ab | Bb | C | D | Eb |
| Ab | Bb | C | Db | Eb | F | G | Ab |
| Db | Eb | F | Gb | Ab | Bb | C | Db |